HL7 (text) File Modification
Q: Good morning, thank you again for taking my call! Please find the before and after test files attached.
- You’ll see that the FT1 segment, specifically the FT1.25 section, was moved to FT1.7 section. (Each section is delimited by a pipe “|”.)
- We also added “CG” (without quotes) to the FT1.6 section. I’ve attached an image to visualize as well.
I’m urgently trying to get this solution in place! Thank you for your help!!!!
A: Summary of what we need to do:
- Load the HL7 (text) File.
- Iterate through the lines in the HL7 File.
- Search for a line that starts with ‘FT1|’.
- Make the requested adjustments.
- Save the HL7 file different from the Source.
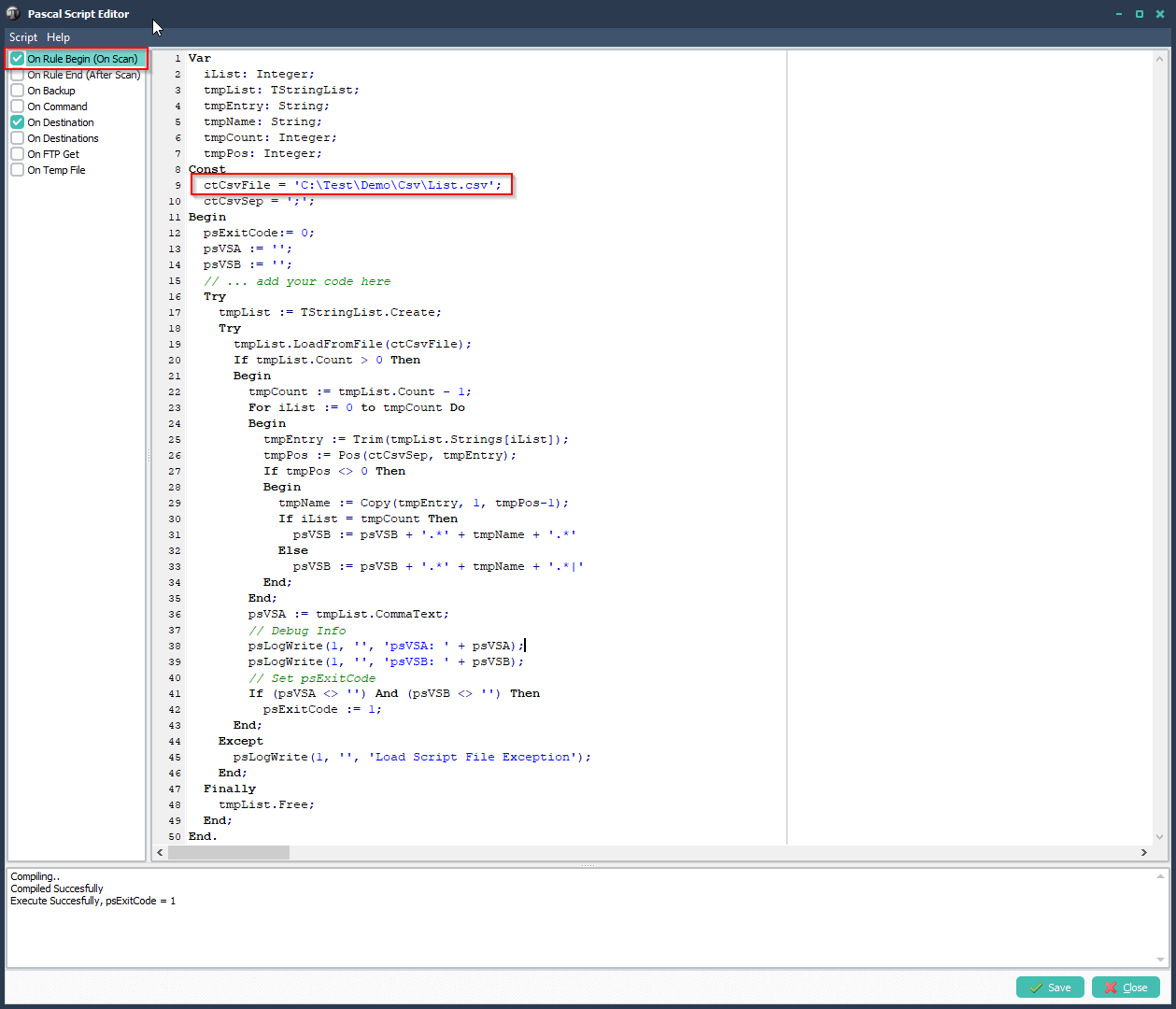
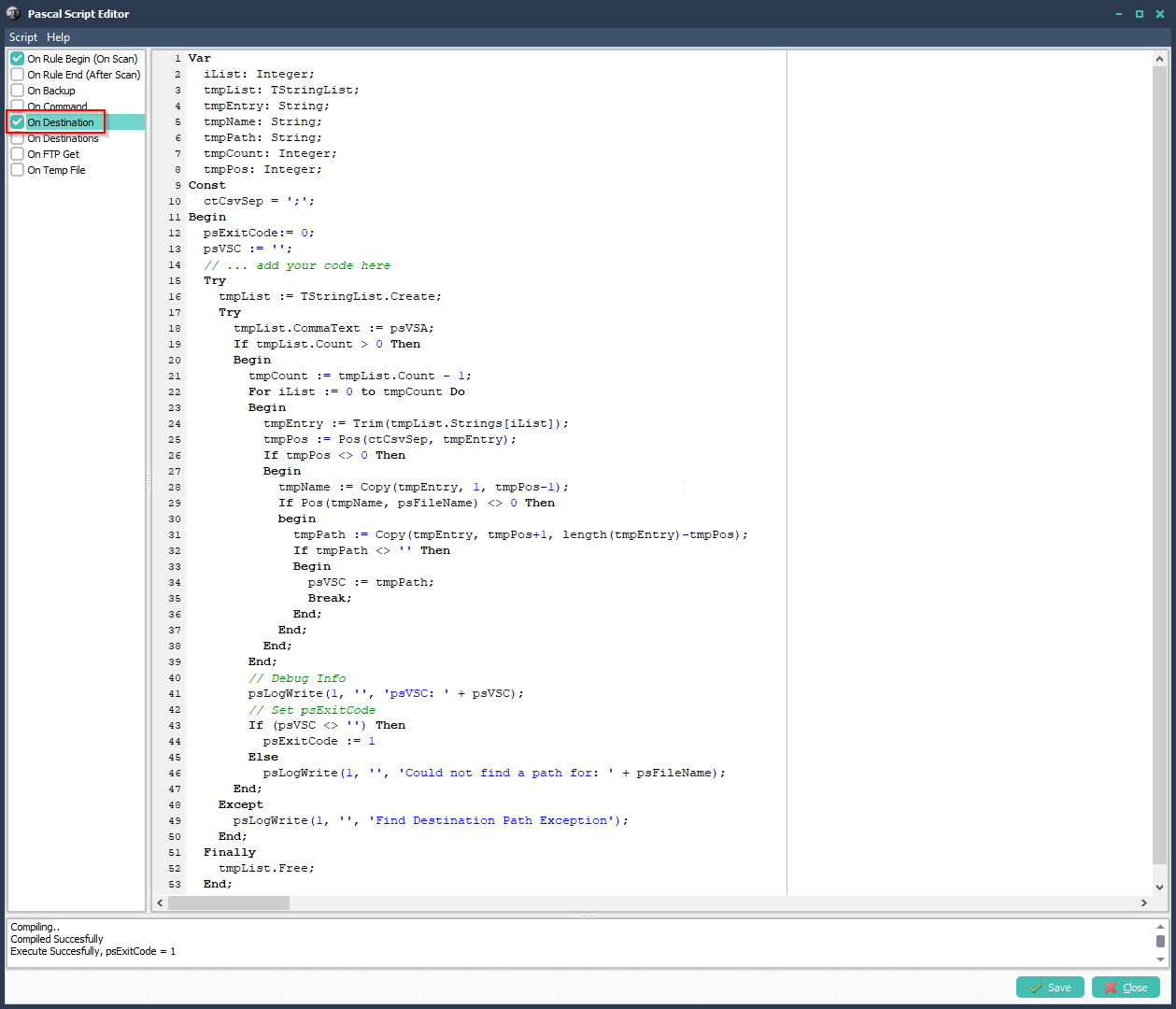
We created a Pascal Script to achieve this (v2021.7.31.0 or higher is needed for this script). Let’s start.
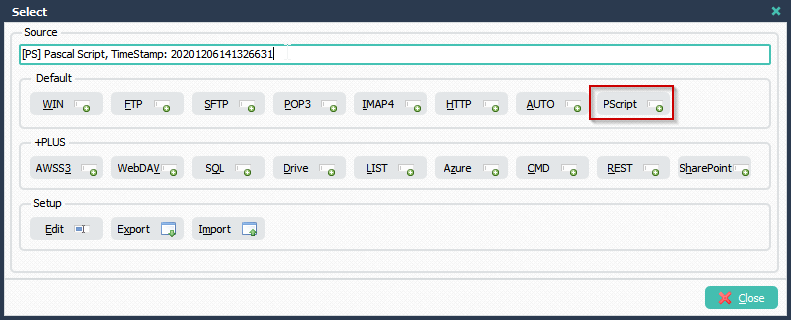
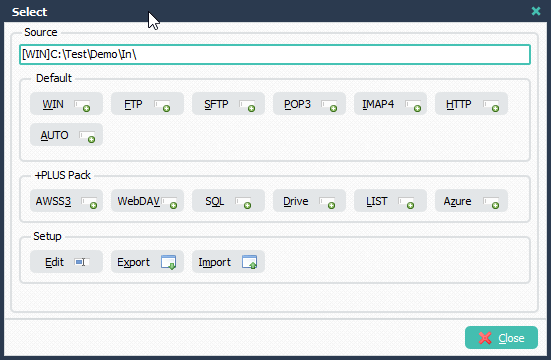
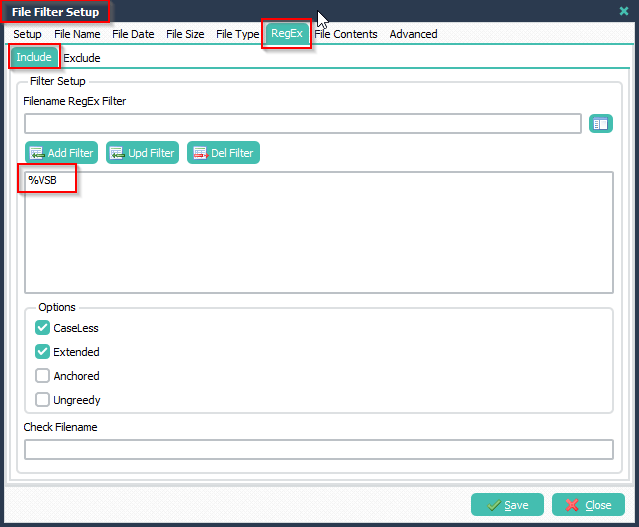
1) Please add a Source and a File Filter for the .HL7 files you want to adjust
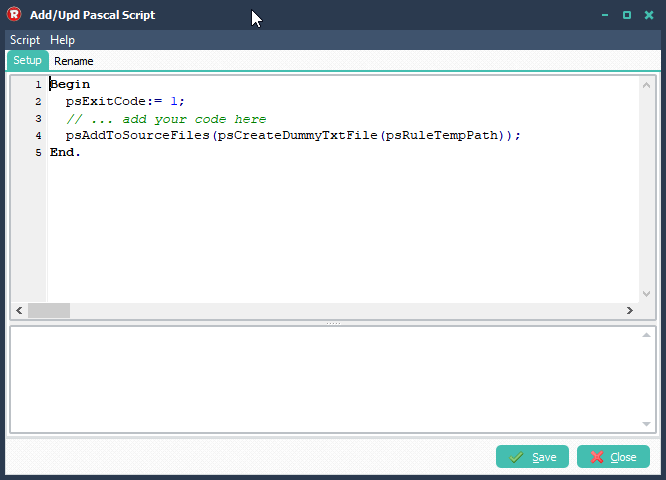
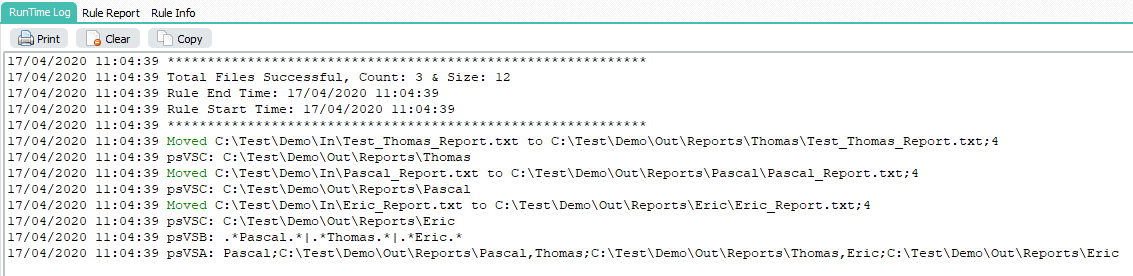
2) Add the following Pascal Script as Destination, don’t forget to adjust the ctOutputPath const ( must end with a \ ).
Var iList: Integer; tmpEntry: String; tmpError: String; tmpField: String; tmpFile : String; tmpList: TStringList; tmpEntryList: TStringList; Const ctOutputPath = 'C:\Test\IN_HL7\Out\'; Begin psExitCode:= 0; // ... add your code here tmpFile := psFilePath + psFileName; tmpList := TStringList.Create; Try Try tmpList.LoadFromFile(tmpFile); // Iterate For iList := 0 to (tmpList.Count-1) Do Begin tmpEntry := tmpList.Strings[iList]; If Pos('FT1|', tmpEntry) <> 0 Then Begin tmpEntryList := psDelimitedTextAsList('|', tmpEntry); If Assigned(tmpEntryList) Then Begin tmpEntryList.Delimiter := '|'; tmpEntryList.StrictDelimiter := True; tmpEntryList.Quotechar := #0; // 0 indexed If tmpEntryList.Count >= 25 Then Begin tmpEntryList.Strings[6] := 'CG'; tmpEntryList.Strings[7] := tmpEntryList.Strings[25]; tmpEntryList.Strings[25] := '' tmpList.Strings[iList] := tmpEntryList.DelimitedText + '|'; // Save To File tmpError := psSaveListToFile(tmpList, ctOutputPath + psFileName, False); if tmpError = '' Then begin psExitCode := 1; psLogWrite(1, '', 'Saved adjusted file to: ' + ctOutputPath + psFileName); End Else psLogWrite(1, '', tmpError); End Else Begin psLogWrite(1, '', 'Field Count error of: ' + tmpEntryList.DelimitedText); End; // Free tmpEntryList.Free; // Break Break; End; End; End; Except psLogWrite(1, '', 'Error loading file: ' + tmpFile); End; Finally tmpList.Free; End; End.
#FileTransfer
Best regards,
Limagito Team